
 |
La realizzazione di un dizionario con tabelle hash si basa sul concetto di ricavare direttamente dal valore della chiave la posizione della chiave stessa. Sia K l’insieme di tutte le possibili chiavi distinte e si memorizzi il dizionario in un vettore D di dimensione m. La soluzione ideale sarebbe quella di possedere una funzione d’accesso (detta funzione hash) che permetta di ricavare la posizione H della chiave k nel vettore D, in modo che:
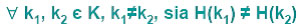
In questo modo ogni chiave avrebbe una posizione ben distinta e univoca. La funzione hash H(k) non fa nient’ altro che generare, in qualche modo, un valore intero H(k) partendo dal valore della chiave k. Per garantire la proprietà indicata sopra occorre però che m (il numero di elementi del dizionario) non sia più piccolo di |K| (il numero delle possibili chiavi). Se il numero delle possibili chiavi è troppo grande, questo metodo è improponibile perché richiede uno spreco enorme di memoria. Occorre quindi tarare la nostra funzione hash sul numero di chiavi attese e non su tutte quelle possibili, ovvero, ammettere che:
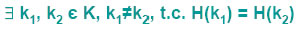
Possono quindi capitare delle chiavi alle quali la funzione hash attribuisce lo stessa posizione. Come risolvere questo problema detto collisione? Occorre calcolare una funzione hash, H(k), che distribuisca uniformemente le chiavi nel vettore D, al fine di ridurre il numero di collisioni. Innanzi tutto la dimensione m del vettore D dovrà essere una sovrastima del numero di chiavi attese al fine di evitare di riempire D; tipicamente m è pari al doppio del numero di chiavi attese. L’algoritmo che calcola H(k) deve fare in modo che la posizione della chiave sia generata nel modo più casuale possibile e che questa generazione sia ripetibile (la funzione applicata ad uno stesso elemento deve dare sempre lo stesso risultato). Si supponga che gli m elementi di D siano indicati da 0 ad m-1; per definire la funzione hash, è conveniente considerare la rappresentazione binaria bin(k) della chiave k. E’ altresì utile denotare con int(b) il numero intero rappresentato da una stringa binaria b. In questo modo oltre a poter agevolmente passare da una chiave alfanumerica alla sua rappresentazione binaria bin(k), si può passare da qualsiasi stringa binaria b ad un numero intero int(b). Date queste condizioni quattro buoni metodi di generazione di indirizzi hash sono i seguenti. I primi tre presuppongono m=2p (una potenza di 2), mentre il quarto presuppone m dispari, meglio se primo.
H(k) = int(b), dove b è un sottoinsieme di p bit di bin(k), solitamente estratti nelle posizioni centrali;
H(k) = int(b), dove b è dato dalla somma modulo 2, effettuata bit a bit, di diversi sottoinsiemi di p bit di bin(k);
H(k) = int(b), dove b è sottoinsieme di p bit estratti in posizione centrale di bin(int(bin(k))2).
H(k) è uguale al resto della divisione di int(bin(k)) per m;
La scelta di estrarre i p bit dalle posizioni centrali è dovuta al fatto che molte chiavi alfanumeriche potrebbero iniziare o terminare con la stessa sequenza di caratteri. Il fatto che m sia primo è per evitare che dividendo si ottenga lo stesso resto e quindi dare vita ad una collisione. Oltre ad una buona funzione hash, occorre inoltre un metodo di scansione che permetta di posizionare e reperire le chiavi che hanno trovato la propria posizione occupata (le collisioni inevitabili). I metodi di scansione si distinguono in esterni e interni, a seconda che le chiavi siano memorizzate all’esterno o all’interno del vettore D. Per saperne di più consulta i seguenti approfondimenti:
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.