
 |
Data una interrogazione q da realizare in algebra relazionale, a volte la si può scomporre in sotto-interrogazioni che possono corrispondere a diversi idiomi. Molti di questo idiomi si basano sul principio di complementarietà:
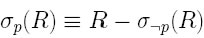
La selezione fatta su una relazione R con un predicato p, è uguale alla relazione R stessa meno la selezione su R con predicato p negato.
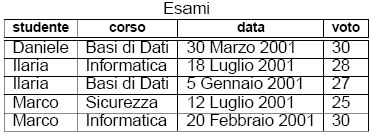
Per esempio nella relazione ESAMI, l’ insieme degli studenti che ha preso 30 è dato dall’ insieme di tutti gli studenti che hanno dato almeno un esame (quelli nella tabella ESAMI) meno tutti gli studenti che non hanno preso 30. Gli idiomi di interrogazione principali sono:
Minimo/massimo assoluto
Dato lo schema relazionale R(A;B) trovare il minimo/massimo B in R
Supponiamo di determinare il minimo:
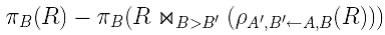
Nella seconda parte vengono trovati tutti quei valori che non sono il minimo. Per far questo viene fatto un join tra le relazione R e se stessa, con però tutti gli attributi rinominati. La condizione di join dice che ogni attributo B deve essere maggiore degli stessi attributi rinominati. In questo modo vengono tenute tutte le tuple tranne quella in cui l’ attributo B assume il valore minore. Quindi per il principio di complementarietà sottraendo dall’ insieme iniziale, l’ insieme delle tuple dove B non è il minimo, otteniamo proprio il valore minimo che cercavamo. Nel caso che la relazione R fosse la relazione Esami, e l’ attributo B sia voto, allora il risultato dell' espressione algebrica scritta sopra sarà 25.
Minimo/massimo relativo
Dato lo schema relazionale R(A;B) trovare per ogni A il minimo/massimo B in R. Supponiamo di determinare il massimo:
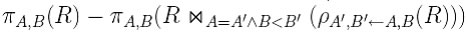
E' molto simile al massimo assoluto. Il predicato di join in questo caso seleziona tutti i valori minimi di B per ogni attributo A. Nel caso che la relazione R fosse la relazione Esami, l’ attributo B sia voto e l’attributo A sia nome, allora il risultato dell' espressione algebrica scritta sopra sarà:
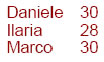
Trovare gli A che sono associati ad almeno 2 B.
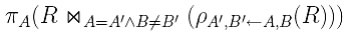
Viene ancora fatto un join tra le relazione R e se stessa, con però tutti gli attributi rinominati. Il predicato del join permette di mantenere tutte quelle tuple in cui l’ attributo A è uguale e B è diverso. Queste tuple sono proprio tutte le tuple di B associate almeno due volte ad ogni elemento di A.
Trovare gli A che sono associati ad almeno 3 B
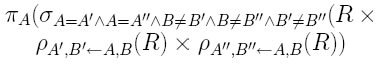
Viene fatto il prodotto cartesiano della relazione e dei suoi due duplicati con gli attributi rinominati. Dalla relazione che otteniamo cosi facendo, vengono selezionate le tuple che soddisfano il predicato di selezione, ovvero tutte le tuple in cui A è associato ad almeno 3 B. I generale per trovare gli A che sono associati ad almeno n B dobbiamo fare:

Trovare gli A per i quali tutti i C sono positivi
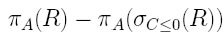
A tutti gli A togliamo quegli A per cui C è negativo ottenendo cosi gli A per i quali tutti i C sono positivi.
Trovare gli A per i quali tutti i C sono uguali
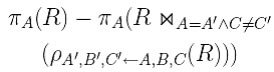
Il join permette di trovare tutti gli elementi di A che non hanno tutti i C uguali. Sottraendo ciò che troviamo dal join con l' insieme di tutti gli elementi, otteniamo gli A per i quali tutti i C sono uguali.
Dati gli schemi relazionali R(A;B) e S(B) trovare gli A per i quali l’insieme dei B associati include tutti gli elementi di S.
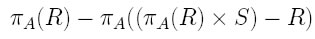
Per comprendere meglio vediamo il seguente esempio:

Nel prodotto cartesiano vengono calcolati tutti le possibili combinazioni tra studente e corso. Sottraendogli tutti gli esami veramente superati ci rimangono solo gli studenti che non hanno superato tutti gli esami. Sottraendo all’ insieme degli studenti quelli che non hanno superato tutti gli esami, otteniamo proprio tutti gli studenti che hanno superato tutti gli esami.
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.