
 |
Nel calcolo dei cammini minimi per ottenere una procedura efficiente, non basta che la struttura dati S utilizza sia un generico “insieme” con un’ altrettanto generica operazione “leggi”, ma occorre specificarle ulteriormente (vedi funzione SPT scritta in linguaggio C).

Se l’insieme S è una coda di priorità realizzata con uno heap, si ottiene l’algoritmo proposto da Johnson (1977). Gli elementi di S sono i nodi u con priorità data dal valore du. La principale difficoltà dell’algoritmo di Johnson è quella di mantenere “aggiornate” le priorità degli elementi che sono decrementate con l’assegnamento d[v] = d[u] + c[u,v]. Infatti nella struttura standard dello heap, gli elementi coincidevano con le priorità, invece nel nostro caso gli elementi sono nodi del grafo, le priorità le distanze dei nodi da r. Lo heap va quindi mantenuto ordinato secondo le priorità utilizzando una nuova operazione che possiamo chiamare decrementa. Questa operazione sarà sintatticamente e semanticamente di questo tipo.

Se cuv >= 0, allora l’algoritmo ha complessità polinomiale in quanto ogni nodo viene estratto da S una ed una sola volta. Il ciclo while ha complessità O(n), mentre gli operatori heap O( log n). Nel caso pessimo decrementa viene chiamata ad ogni iterazione su tutti i nodi in A(u) (nodi adiacenti ad u). Allora complessità risulta:
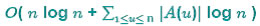
Visto che
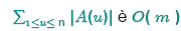
dove m è il numero di archi allora la complessità dell’algoritmo è O( m log n). Si noti che in alcuni casi l’ algoritmo di Johnson è più veloce di quello di Dijkstra.

Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.