
 |
|
Per codificare i numeri interi, positivi e negativi, viene indicato prima il segno, seguito poi dal valore assoluto. Questa rappresentazione chiamata codifica con modulo e segno, utilizza il primo bit per indicare il segno (0 positivo e 1 negativo) e gli altri n-1 bit per la rappresentazione del valore assoluto del numero.
Base |
Base |
Base |
Base |
||||
due |
dieci |
due |
dieci |
due |
dieci |
due |
dieci |
0000 |
0 |
0100 |
4 |
1000 |
-0 |
1100 |
-4 |
0001 |
1 |
0101 |
5 |
1001 |
-1 |
1101 |
-5 |
0010 |
2 |
0110 |
6 |
1010 |
-2 |
1110 |
-6 |
0011 |
3 |
0111 |
7 |
1011 |
-3 |
1111 |
-7 |
Con n bit, questa codifica consente di rappresentare i numeri
interi da -2n-1-1 a 2n-1 -1. Questa codifica ha però il
difetto di duplicare la rappresentazione del numero 0, come se -0 fosse diverso
da +0. Si preferisce quindi utilizzare la codifica detta rappresentazione
in complemento a due: dati n bit per rappresentare un numero x si utilizza
il valore binario corrispondente a 2n+x. Con successioni di 4 bit
in cui 2n è quindi 16, per esempio, la rappresentazione del numero
5dieci diventa 16dieci+5dieci =21dieci=10101due.
Siccome sono disponibili solo 4 bit , viene tolto il bit più significativo,
conservando solo 0101due, che corrisponde peraltro alla codifica
binaria del numero naturale 5dieci. Se invece si vuole rappresentare
un numero negativo, per esempio -5dieci, si ottiene 16dieci-5dieci=11dieci=01011due,
da cui si ottiene 1011due.
Base |
Base |
Base |
Base |
||||
due |
dieci |
due |
dieci |
due |
dieci |
due |
dieci |
0000 |
0 |
0100 |
4 |
1000 |
-8 |
1100 |
-4 |
0001 |
1 |
0101 |
5 |
1001 |
-7 |
1101 |
-3 |
0010 |
2 |
0110 |
6 |
1010 |
-6 |
1110 |
-2 |
0011 |
3 |
0111 |
7 |
1011 |
-5 |
1111 |
-1 |
Si può notare come il primo bit dei numeri positivi sia 0, mentre i numeri negativi hanno il primo bit uguale a 1. Il numero 0 ha ora una rappresentazione unica, anche se ciò impedisce di bilanciare i numeri positivi con quelli negativi (con 4 bit sono stati rappresentati 8 numeri negativi e solo 7 positivi). In generale, con questa codifica, n bit sono sufficienti per rappresentare i numeri che vanno da -2n-1 fino a 2n-1-1. Nel caso della codifica binaria in complemento a 2, avendo un numero positivo espresso in base due, per ottenere il suo negativo dovrò complementare (cambiare di valore) ogni singolo bit e sommargli uno (vedi somma di numeri binari). Per esempio:
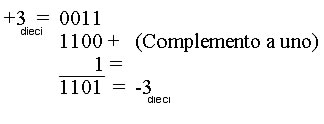
La codifica in complemento a 2 è molto utile, in quanto permette di eseguire solo somme. Per esempio si voglia eseguire 2 - 4. E' uguale a scrivere +2 + (-4):
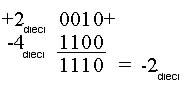
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.