|
|
|
Occorre spesso trattare con numeri razionali o reali.
Si pensi al valore di 1/3=0.33333…dieci. Poiché nella rappresentazione
a uso di un esecutore automatico sono utilizzabili solo successioni di bit di
lunghezza finita, è necessario approssimare numeri di questo genere. E' utile
allora definire il concetto di cifre più significative: nelle rappresentazioni
basate sulla notazione
posizionale, le cifre più significative sono quelle associate a pesi maggiori.
Per esempio nel numero 654 321dieci, la cifra più significativa è
6 associata al peso 105. Ne caso dei numeri minori di 1, che iniziano
con 0 seguito dal separatore decimale, le cifre più significative sono quelle
diverse da 0 poste più a sinistra . Per esempio nel numero 0.0065432dieci,
la cifra più significativa è 6, con peso 10-3. Un ulteriore problema
riguarda la rappresentazione di numeri con valore assoluto molto grande o molto
piccolo. In questi casi si considerano solo le cifre più significative, adottando
una rappresentazione che viene indicata come notazione scientifica,
per cui un numero in base 10 viene rappresentato come ±m x 10e(più
generalmente come ±m x Be in base B). Si procede quindi indicando
il segno (+ oppure -), il coefficiente m, detto mantissa
(dove si adopera la convenzione di inserire una virgola decimale subito dopo
la prima cifra), e l'esponente e a cui elevare la base di numerazione.
Il numero -123 450 000 000dieciviene quindi rappresentato come -1.2345
X 1011 dieci; il segno è negativo, la mantissa è 12345dieci,
mentre l'esponente è 11dieci. Il numero 0.0000012345 corrisponde
a 1.2345 X 10-6dieci, ha segno positivo, la mantissa è
12345dieci ed esponente -6dieci.
Lo stesso principio viene adottato per la rappresentazione binaria di numeri
razionali: il numero 101010000due corrisponde per esempio a 1.0101
X 101000due, dove il segno è positivo, la mantissa è 10101due
e l'esponente è 1000due (8 in base 10). Questo tipo di rappresentazione
è detto in virgola mobile (Floating Point). Un problema sorge quando
si deve stabilire un numero di bit da utilizzare: cambiando infatti il numero
di cifre dedicato alla rappresentazione di mantissa ed esponente, si può infatti
modificare la precisione dei risultati. L'Institute of Electrical and Electronic
Engineers (IEEE), per
uniformare la precisione di calcolo, ha definito uno standard internazionale
che stabilisce le dimensioni di mantissa ed esponente. Lo standard in questo campo è la codifica IEEE 754, che al suo interno contiene 3 sotto-standard:
Il lettore attento si sarà accorto che il numero 0 non potrebbe
essere rappresentato utilizzando il formato cosi come descritto. Tuttavia,
lo standard riserva alcune configurazioni particolari per quelli che sono
chiamati valori speciali: 0,
,
e
NaN (not a number, risultato indeterminato o numero indefinito):
0 è rappresentato da un numero con un campo esponente tutto di zeri e una mantissa tutta di zeri. Si noti che in tal modo +0 e -0 sono valori distinti, sebbene nei confronti con "=" risultino uguali
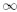è rappresentato
da un campo esponente tutto di uni e una mantissa tutta di zeri.
NaN è rappresentato da un esponente di tutti uni e una mantissa non tutta di zeri.
Lo standard dell'IEEE definisce il risultato delle operazioni aritmetiche che coinvolgono questi numeri speciali come segue:
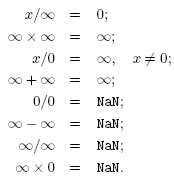
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.