|
|
Il concetto di funzione è uno dei concetti più importante per
la matematica: infatti la matematica è cercare le cause, le implicazioni, le
conseguenze e l'utilità' di una funzione. Siano S e T due insiemi. Si dice che
in S è definita una funzione a valori in T' se è fissata una legge che ad ogni
elemento di S fa corrispondere uno ed uno solo elemento di T.In simboli si scrive
f: S
T.
S può anche essere visto come l'insieme di tutti i punti dell'asse delle ascisse di un piano cartesiano, e T l'insieme di tutti i punti dell'asse delle ordinate.
La x 
S si chiama
variabile indipendente, la y
T si chiama variabile dipendente.
Con altre parole si definisce funzione y della variabile x un legame fra due
variabili, una detta variabile indipendente x e l'altra detta variabile dipendente
y, tali che abbiano senso le operazioni da effettuare sulla x per ottenere
i valori della y e per ogni valore della x corrisponda un solo valore della
y.
y=f(x)
L'insieme dei valori che può assumere x (S) è detto
"dominio" della variabile indipendente o "campo di esistenza" della
funzione; l'insieme dei valori assunti dalla variabile dipendente y è detto
campo di variabilità della funzione o "condominio". Si chiama Grafico
o diagramma di una funzione il sottoinsieme G di S x T costituito da tutte
le coppie del tipo (x, f(x)) al variare di x in S.
Sia X insieme 
S
e f: S T una funzione; si definisce
immagine di x, mediante f, il sottoinsieme di T costituito da tutti gli elementi
che sono immagini degli elementi di x.
Nel caso in cui serve determinare un elemento di S partendo
da T, si utilizza il concetto di inversione della funzione indicato
con f -1. Sia f: S T
e Y un sottoinsieme di T (Y T), si
chiama controimmagine di Y il sottoinsieme di S costituito dagli elementi
X che hanno immagine appartenente a Y.
Se f: S 
T, ovvero se gli elementi
di S coincideranno con quelli di T, cioè l'applicazione della funzione su
tutti gli elementi dell'insieme S produce tutti gli elementi dell'insiemi
T, la funzione si dice surjettiva. Sia f: S
T, se scelti X1 e X2 S, diversi
tra loro X1 
X2, si ha f(X1)
f(X2) la funzione si dice injettiva
(se e solo se elementi distinti cadono in elementi distinti). Nel caso in
cui una funzione è contemporaneamente surjettiva che injettiva, viene chiamata
bijettiva. Se nella funzione f(x) (f: S
T), scambiando x con -x la funzione non presenterà cambiamenti, la funzione
è detta pari f(x) = f(-x). Ad esempio y = x2 . Allo
stesso modo si dirà dispari se 
x
S f (x) = - f (x); in questo
caso c'è un cambio di segno tra origine e trasformata. C'è da notare che
non esistono solo funzioni esclusivamente pari od esclusivamente dispari,
ogni funzione può essere suddivisa nella somma di una funzione pari ed una
dispari. Una funzione composta è una funzione
di una funzione g(f(x)) ed è indicata con g o f. Per la costruzione della
funzione composta saranno necessari 3 insiemi, di cui uno farà da "intermediario"
tra i due posti agli estremi. Siano quindi:
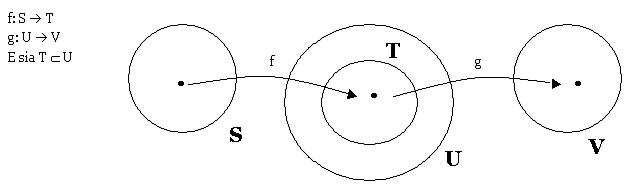
g[f (x)] è quindi l'immagine di f (x) mediante la g. Questa
legge di composizione, in genere, non sarà commutativa; quindi:
g[f (x)]
f[g (x)]. Prendendo infatti:
In generale quindi g[f (x)] f[g (x)]
Per saperne di più consulta i seguenti approfondimenti:
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.