|
|
Due gruppi (A, #) e (A', @) si dicono omomorfi se esiste una
applicazione f tra gli insiemi A e A' tale che per ogni a, b 
A risulti:
f (a # b) = f(a) @ f(b)
Come per ogni applicazione, A si dice dominio e A' codominio
dell'omomorfismo.
Ogni omomorfismo f gode delle seguenti proprietà:
Associa all'elemento neutro di un gruppo l'elemento neutro dell'altro:
infatti, se u è l'elemento neutro di A, per ogni elemento a
A risulta
u # a = a # u = a
f(u # a) = f(a # u) = f(u) @ f(a) = f(a) @ f(u)
e poiché u è elemento neutro di A,
f(u # a) = f(a # u) = f(a),
dunque
f(a) = f(u) @ f(a) = f(a) @ f(u)
Questa proprietà è una comoda condizione necessaria: se non vale, sicuramente
la applicazione non è un omomorfismo.
Ogni omomorfismo f associa all'inverso di un elemento in A l'inverso
dell'immagine di quell'elemento in A':
Infatti per ogni a A risulta
f(a # a-1) = f(u) = u',
ma per l'omomorfismo deve risultare
f(a # a-1) = f(a) @ f(a-1) = u'
cioè
f(a-1) = [f(a)]-1.
Se f risulta biunivoca l'omomorfismo si chiama isomorfismo.
Due gruppi finiti che abbiano un diverso numero di elementi possono essere omomorfi
ma non isomorfi, perché tra essi, ovviamente, non è possibile alcuna corrispondenza
biunivoca. Dire che due gruppi sono isomorfi significa che esiste un isomorfismo
tra i gruppi, non che ogni omomorfismo sia un isomorfismo.
L'immagine di un elemento a è un elemento
a'.
DEFINIZIONE. Si chiama immagine di A nell'omomorfismo f(A,#)->(A',@),
e si indica con f (A) o con Imf, il sottoinsieme di (A',@)
costituito dai trasformati degli elementi di A.
Teorema: Dato un omomorfismo di gruppi f:(A,#)->(A',@), l'immagine
Imf è sottogruppo del codominio.
DEFINIZIONE. Si chiama nucleo di
un omomorfismo f tra due gruppi (A,#) e (A',@) il sottoinsieme di (A,#)
costituto da tutti gli elementi tali che f(a) = u', essendo u' l'elemento
neutro di A'. Il nucleo è indicato con ker(f ).
Teorema: Dato un omomorfismo di gruppi f (A,#)->(A',@), il nucleo ker(f)
è sottogruppo del dominio.
Teorema: Dati due gruppi finiti (A,#) e (A',@), il primo di ordine h, il secondo k. Sia f un omomorfismo tra i due gruppi. Allora : ord(ker(f)) x ord(f(A)) = ord(A).
Vediamo come esempio il seguente esercizio:
Si consideri il gruppo S7 delle permutazioni sugli elementi 1, 2, ... ,7
Scrivere la permutazione 
=(1 3 6 2)(4 3 6)(3 5 7)(1 5 7 2) come prodotto di cicli disgiunti e stabilire
se è pari o dispari
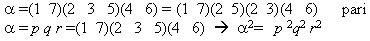
Determinare l'ordine del sottogruppo X di S7
generato da e indicarne gli elementi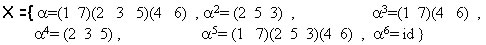
Determinare tutti i possibili omomorfismi di (Z6,+)
in X
(Z6,+) ={0, 1, 2, 3, 4, 5} è il dominio ed è ciclico con generatore 1
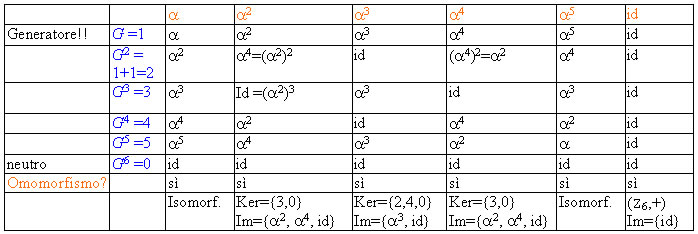
In blu riportiamo gli elementi del dominio ordinati secondo le loro potenze.
In rosso gli elementi del codominio ordinati a piacere.
Se G va in a, G2 andrà in a2 e cosi via……..fino a G6 che va in Id. Essendo che l'elemento neutro va nell'elemento neutro per la sopra citata proprietà abbiamo un omomorfismo.
Essendoci una corrispondenza biunivoca, ovvero tutti gli elementi cadono in tutti gli elementi l'omomorfismo è un isomorfismo.
Se G va in a2, G2 andrà in a4 e cosi via fino a G6 che va in Id. Essendo che l'elemento neutro va nell'elemento neutro per la sopra citata proprietà abbiamo un omomorfismo.
In questo caso non abbiamo un isomorfismo, in quanto non c'è una corrispondenza biunivoca.
Il nucleo è è sottogruppo del dominio costituto da tutti gli elementi tali che f(a) = u' essendo u' l'elemento neutro del codominio, quindi in questo caso Ker={3,0}
L'immagine è sottogruppo del codominio costituito dai trasformati degli elementi del dominio, quindi in questo caso Im={a2, a4, id}
………
………
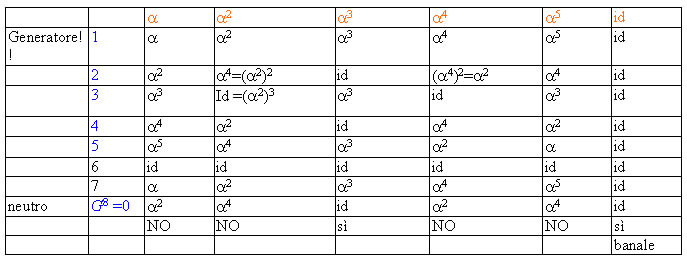
Determinare tutti i possibili omomorfismi di (Z8,+) in X
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.