Le definizioni ricorsive

Oltre alle dimostrazioni per induzione, si possono dare anche definizioni per ricorrenza o definizioni ricorsive: come il principio di induzione sono costituite da due affermazioni:
una che stabilisce in modo esplicito il primo elemento,
l'altra che definisce l'elemento generico mediante i precedenti.
Di seguito alcuni esempi:

ESEMPIO 1

Operazione di elevamento a potenza di un numero naturale a > 0: 1) a0 = 1

1) a⁰ = 1
2) aⁿ = a^n-1 ·a

ESEMPIO 2

Un'altro esempio di definizione ricorsiva si può fare con la successione di Fibonacci:

1) a₀=0, a₁=1
2) a_n = a_n-1 + a_n-2

ESEMPIO 3

Anche ad un numero fattoriale si può assegnare una definizione ricorsiva. Proviamo a pensare a quanti sono tutti i possibili anagrammi (anche privi di senso) di una data parola. La risposta dipende dal numero n di lettere, che supponiamo differenti.
con 1 lettera abbiamo 1 anagramma soltanto: a
con due lettere 2 anagrammi (2·1): ad, da
con 3 lettere, 6 anagrammi (3·2·1): ape, aep, pae, pea, eap, epa.
con 4 lettere 24 anagrammi (4·3·2·1):
rosa, roas, rsoa, rsao, raos, raso,
orsa, oras, osra, osar, oars, oasr,
sroa, srao, sora, soar, saro, saor,
aros, arso, aors, aosr, asro, asor.
Gli anagrammi sono le permutazioni di n oggetti. Il numero di permutazioni di n oggetti è 1·2·3· ...·n.
Questo numero si chiama fattoriale di n, si indica con il simbolo n!. La definizione ricorsiva di n! sarà:

1) 1! = 1
2) n! = (n - 1)!·n.

Risulta utile definire anche 0!; si pone per convenzione 0!=1, e allora la definizione ricorsiva si modifica nel seguente modo:

1) 0! = 1
2) n! = (n - 1)!·n.

ESEMPIO 4

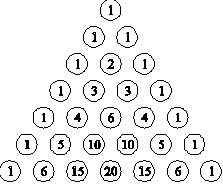
Anche al triangolo di Tartaglia può essere attribuita una definizione ricorsiva, in quanto ogni elemento è la somma dei due numeri della riga precedente che gli "stanno sopra", a destra e a sinistra.

Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.