
 |
Le possibile sequenze di confronti a due alternative effettuate da un algoritmo per risolvere un problema possono essere visualizzate con un albero binario, detto albero decisionale.
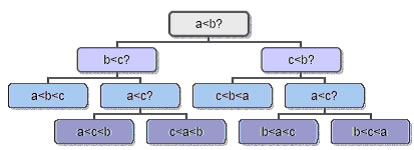
In un albero cosi composto:
i nodi con figli rappresentano confronti tra dati del problema;
le foglie rappresentano soluzioni possibile del problema;
le coppie padri-figli rappresentano i risultati dei confronti.
Osserviamo che un percorso radice->foglia rappresenta una sequenza di confronti effettuati per raggiungere una soluzione. Il livello massimo di una foglia è uguale al numero di confronti effettuati nel caso pessimo, per raggiungere una soluzione. Questa è una misura di complessità.
Quindi l’ albero di decisione che minimizza il livello massimo delle foglie fornisce, con tale valore m, una limitazione inferiore al numero di decisioni che ogni algoritmo deve effettuare nel caso pessimo (l ‘algoritmo deve effettuare almeno m decisioni nel caso pessimo).
L’ albero decisionale può essere allora utilizzato come strumento per determinare la complessità di un problema.
Proviamo ad analizzare la complessità del problema di ordinare n numeri con un albero di decisione.
Un qualsiasi algoritmo di ordinamento di n numeri deve fare una sequenza di scelte che permetta di individuare la soluzione corretta tra le n! permutazioni possibili dei dati d’ ingresso.
Quindi l’ albero di decisione corrispondente avrà almeno n! foglie.
Considerando che a ogni livello i nodi al più raddoppiano, la massima lunghezza del percorso radice->foglia non può essere inferiore a log2n!
Essendo:
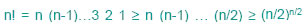
allora per le proprietà dei logaritmi:
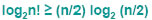
Pertanto una limitazione inferiore alla complessità del problema dell’ ordinamento è:

Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.