
 |
L’ algoritmo di Knuth Morris Pratt è un algoritmo che utilizza la tecnica di “Backtrack” , per risolvere il problema dello String Matching. L’idea principale è quella di trarre giovamento della computazione svolta prima di fare backtrack. Ovvero, dopo aver riconosciuto j-1 caratteri del pattern P (dove j è l ‘indice utilizzato per scandire P) perché tornare indietro di j-2 posizioni? Non è possibile utilizzare i confronti già effettuati? Osserviamo il seguente esempio:
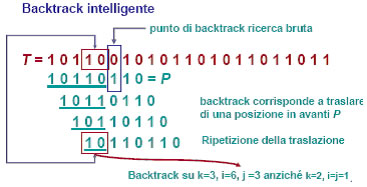
al momento del primo backtrack i = 6 e j = 6. Ripartire come nella ricerca “bruta” con i = 2 e j = 1 corrisponde a traslare a destra di una posizione il pattern rispetto al testo. Ma ciò corrisponde anche a traslare a destra di una posizione rispetto a se stessa la sottosequenza di P riconosciuta nel testo, ovvero 10110. In questa sottosequenza i primi quattro caratteri non coincidono con gli ultimi quattro ed è per tanto inutile ripartire con i = 2. Inoltre anche i primi tre non corrispondono con gli ultimi tre e quindi è altrettanto inutile ripartire da i = 3. I primi due caratteri della sottosequenza coincidono in vece con gli ultimi due e pertanto conviene ripartire con i = 4. poiché i successivi due caratteri di P coincidono sicuramente con quelli di T, tanto vale ripartire con i = 6 e j = 3. Si considerano due copie dei primi j-1 caratteri del pattern P, e si immagini di disporle orizzontalmente una sotto l’ altra, in modo che il primo carattere della coppia inferiore stia sotto il secondo della copia superiore. Se tutti i caratteri sovrapposti non sono uguali, si traslano di una posizione a destra tutti i caratteri della copia inferiore. Si arresti questo procedimento non appena tutti i caratteri sovrapposti delle due copie siano identici. Il nuovo valore di “backtrack” da assegnare all’ indice j, che indichiamo con back[j] è proprio uguale al numero di caratteri sovrapposti più uno (se non ci sono caratteri sovrapposti risulta ovviamente uguale a uno).
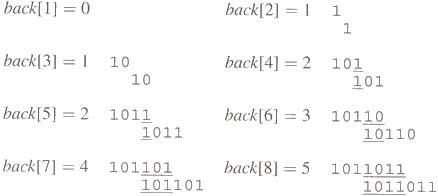
Nel nostro esempio, al momento del primo backtrack i = 6 e j = 6. I j-1 = 5 caratteri riconosciuti del pattern sono 10110. Con la tecnica analizzata sopra otteniamo:
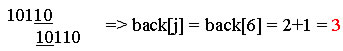
Infatti all’ indice j, come visto sopra, verrà assegnato il valore 3, j = 3. In modo più formale e matematico possiamo definire back[ j ], il nuovo valore di backtrack da assegnare all’indice j, valore dato da:
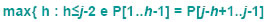
Sempre nel nostro esempio il massimo h è proprio 3, infatti P[1…h-1] = 10 che è uguale a P[j-h+1…..j-1] = P[6-3+1….6-1] = 10. La posizione dell’ indice i non viene modificata e pertanto dopo il primo backtrack eseguiremo il confronto con i = 6 e j = 3. In linguaggio C possiamo implementare questo algoritmo nel seguente modo:

La funzione KMP restituisce, una volta trovata la stringa, la posizione i – m di inizio del pattern in T. Innanzi tutto è introdotto in fase di inizializazione il calcolo del vettore back, effettuato con la funzione calcola_back.

Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.