Greedy

La tecnica di progettazione di algoritmi di tipo Greedy, si basa sulla semplice strategia dell’ ingordo, ovvero, quella di compiere, ad ogni passo, la scelta migliore nell’immediato piuttosto che adottare una strategia a lungo termine. Gli algoritmi di tipo Greedy sono particolarmente indicati per la soluzione di quei problemi nei quali è prevista la selezione di un sottoinsieme S “ottimo” di elementi, che verificano certe proprietà, da un insieme dato (a1…………an). Uno schema generale di questo algoritmo potrebbe essere il seguente:

Un algoritmo Greedy quindi ordina dapprima gli oggetti in base al criterio di ottimalità. La soluzione del problema è poi costruita in modo incrementale considerando gli oggetti uno alla volta ed aggiungendo, se possibile, l’oggetto migliore secondo il criterio di ottimalità. L’ algoritmo effettua quindi una sequenza di scelte, preferendo ogni volta la scelta che fornisce immediatamente il miglior risultato. Vediamo l’ esempio del bin packing, ovvero dati n oggetti a_i di peso p_i, partizionare gli n oggetti in contenitori Bk (bin) di capacità C tale che il numero totale k di bin sia minimo. Nella fase di Ordinamento vengono disposto gli elementi decrescenti rispetto al peso. La soluzione del problema è poi costruita in modo incrementale, infatti nella costruzione dell’ insieme S, viene posta le seguente condizione: inserisci a_i in Bk scelto in modo che sia minimo.

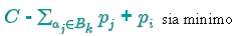
ovvero la differenza tra la capacità del contenitore C e la sommatoria dei pesi degli elementi a_j appartenente al contenitore B + il peso dell’ elemento a_i, deve essere minima. Infatti se ogni contenitore B ha il minor spazio libero anche il numero k dei contenitori sarà minimo. In sintesi, in un algoritmo Greedy, le scelte sono fatte in base ad un principio di ottimalità locale e ad ogni passo viene risolto un sottoproblema di dimensioni sempre più piccole. La sua soluzione dipende dalle scelte passate ma non da quelle future. Affinché un algoritmo di tipo Greedy fornisca la soluzione ottima di un dato problema occorre che siano verificate due proprietà tra loro correlate:

Scelta Greedy: Data una caratterizzazione matematica della soluzione, occorre dimostrare che tale soluzione può essere modificata in modo da utilizzare una prima scelta greedy per ridurre il problema ad un sottoproblema più piccolo dello stesso tipo.
Sottostruttura ottima: Per mostrare che una scelta greedy riduce il problema ad un sottoproblema più piccolo dello stesso tipo, occorre dimostrare che una soluzione ottima del problema contiene al suo interno le soluzioni ottime dei sottoproblemi.

In genere gli algoritmi di tipo greedy non forniscono una soluzione ottima per un dato problema, ma noi vedremo di seguito due algoritmi greedy ottimi per:

Inoltre molti dei problemi per i quali un algoritmo di tipo greedy fornisce una soluzione ottima, possono essere formulati come Matroidi.

Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.