Scheduling di programmi

La tecnica greedy è spesso utile per risolvere problemi di scheduling, in cui si hanno dei programmi da eseguire su un processore e si vuole trovare l’ ordine di esecuzione ottimo in base ad un prefisso criterio. Immaginiamo un problema di scheduling del seguente tipo. Dati n programmi p,…,p_n tali che ciascun p_i richiede t_i unità di tempo per la sua esecuzione e deve essere completato entro una certa scadenza d_i, trovare un ordine S in cui eseguire tutti i programmi in modo da minimizzare il numero di programmi per i quali la scadenza non è rispettata. Il problema può essere risolto con un algoritmo di tipo greedy ideato da Moore nel 1968. I programmi sono ordinati in una sequenza S per scadenze crescenti.

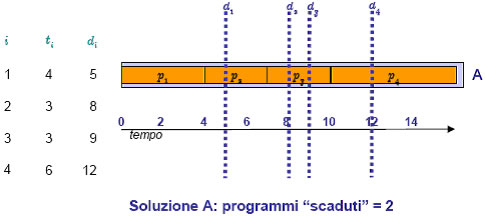
Si scorre la lista per identificare il primo programma p’ in ritardo; si elimina il programma p” più lungo che precede p’. Si itera il procedimento fino ad ottenere una sequenza S priva di programmi in ritardo. La sequenza S ottima è ottenuta aggiungendo, in un ordine qualsiasi, i programmi precedentemente eliminati.

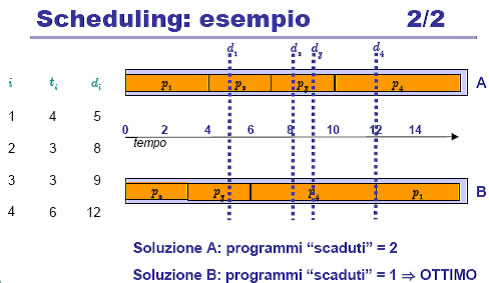
Una realizazione poco accorta dell’ algoritmo porta ad una complessità di O(n²). Infatti si possono calcolare, per tutti i programmi p della sequenza S, gli istanti in cui terminano la loro esecuzione. Tali istanti sono dati dalla somma dei tempi di esecuzione di p e dei programmi che lo precedono.

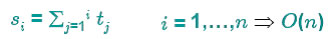
Tale calcolo richiede O(n) tempo per tutti i programmi. Confrontando poi gli istanti di terminazione dei programmi con le rispettive scadenze, si può determinare il primo programma p in ritardo e quindi eliminare il programma p più lungo. Anche questa fase richiede O(n) tempo. Poiché il procedimento di eliminazione di un programma si potrebbe iterare per O(n) volte, la complessità risulterebbe appunto O(n2). La complessità può essere migliorata attraverso l’uso di una coda di priorità. Q implementata con uno heap modificato. Un programma alla volta è inserito in Q con chiave ti. Se si >= di (l’ istante di terminazione di un programma è maggiore della scadenza , e quindi il programma p_i in ritardo), si estrae dalla coda il programma j con chiave (t_j) massima e si aggiorna s_i. Vediamo di seguito una possibile implementazione in linguaggio C:

Questa funzione utilizza due vettori d[1….n] e t[1….n ] per le scadenze ed i tempi di esecuzione degli n programmi. Utilizza poi un vettore bollano r [1…n] tale che r_i = true solo se il programma i è in ritardo. Viene poi utilizzata una variabile intera T per calcolare la somma dei tempi di esecuzione dei programmi inseriti in Q. Quando T >= d[i] allora il programma i è in ritardo, e viene estratto da Q, il programma j con tempo di esecuzione massima max(Q), sottraendo poi t_j da T, incrementando K, e impostando r[j] a true. Al termine dell’ esecuzione la variabile k contiene il numero dei programmi in ritardo, mentre il vettore r specifica quali programmi sono o non sono in ritardo. La sequenza ottima è ottenuta eseguendo dapprima i programmi con r[j] = false in oridne di indici cresecenti, e poi gli altri in un ordine qualsiasi. L’ordinamento iniziale costa O(n log n ). Il ciclo for è ripetuto n volte e ogni iterazione del ciclo costa O( log n ) sia per l’inserimento in Q che per cancellamax e max. Inoltre la sequenza ottima S* può essere ottenuta in O(n) tramite una scansione . Pertanto la complessità dell’ algoritmo di Moore è (n log n).

Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.