
 |
Una struttura dati che opera su un insieme è il cosiddetto merge-find-set, brevemente Mfset, ovvero insieme trova e fondi. Mfset rappresenta una partizione di un insieme finito in sottoinsiemi disgiunti, detti componenti o parti. Le operazioni ammesse permettono di stabilire a quale componente appartiene un generico elemento e di unire due componenti distinti. La diversità rispetto all’ usuale tipo di dato insieme consiste nel fatto che non sono previste cancellazioni o inserzioni. Le operazioni cocesse sono le seguenti:
Creamfset: per inizializzare l’ mfset ad una partizione formata da tanti componenti , contenenti ciascuna un solo elemento;
Trova: restituisce l’ identificatore di un componente;
Fondi: unisce due componenti senza però modificare gli altri, dopo la sua esecuzione il numero totale dei componenti sarà diminuito di uno.
La specifica sintattica di queste operazioni è la seguente:

Dati un insieme A, la specifica semantica con post e precondizioni sarà la seguente:

Per questioni di efficienza ogni elemento dell’ assieme viene realizzata come un albero. Vediamo di seguito una sequenza di fusioni di elementi di un insieme:
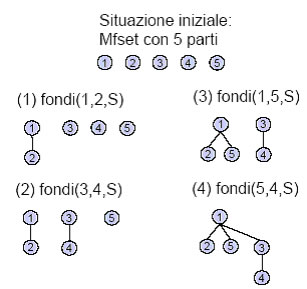
La rappresentazione ad albero determina che la partizione sia rappresentata come un insieme di alberi radicati detta foresta. Ciascun componente è identificato dalla radice dell’ albero corrispondente. Per tanto l’ operatore "trova" si riduce a restituire la radice dell’albero corrispondente. L’operatore "fondi" può essere invece realizzato combinando due alberi in un unico albero. Supponiamo che sia possibile accedere direttamente ai nodi di ogni albero/componente. L’operatore trova si realizza salendo attraverso i padri lungo un percorso da un generico nodo sino ad arrivare alla radice. Analogamente si comporta la fondi, imponendo che una delle due radici divenga il nuovo figlio dell’altra. Si osservi che trova e fondi prevedono entrambe di risalire il cammino nodo -> radice. Una misura di complessità è data quindi dal livello massimo delle foglie di ciascun albero. Per ridurre il livello massimo delle foglie “basta” scegliere come radice di una fondi quella relativa al componente con il maggior numero di nodi. Si impone quindi che la radice di uno degli alberi con il minor numero di nodi divenga un nuovo figlio della radice di quello più grande.Per esempio si consideri la sequenza di fusioni nelle quali un generico elemento x può essere coinvolto e si analizzi di quanto può aumentare, nel caso pessimo, il livello di x. Se x appartiene all’albero più “grande”il livello di x non varia. Se x appartiene all’albero più “piccolo” il livello di x aumenta di 1 ad ogni fondi. Considerato che inizialmente vi sono n=|A| componenti di un unico elemento, le componenti più piccole alle quali x può appartenere e che saranno impegnate in una fusione, sono al più O(log n). Vedi esempio dimostrativo:
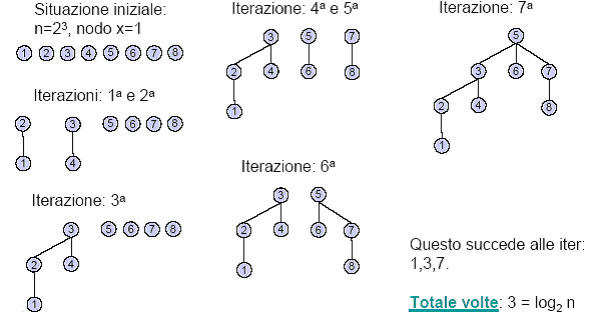
Si noti che se x appartiene all’albero “piccolo”, il numero di nodi della nuova componente ottenuta con fondi è almeno il doppio di quelli dell’albero cui x apparteneva (nel nostro caso fondiamo alberi di uguali dimensioni). In conclusione, considerato che ad ogni fusione il livello delle foglie dell’albero più “piccolo” aumenta di uno, che inizialmente il generico elemento x è a livello 0, e che il livello del nodo x risulta essere O(log n) nel caso pessimo; di conseguenza, la complessità di trova e fondi è O(log n). Per saperne di più consulta i seguenti approfondimenti:
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.