
 |
Un albero 2-3 è un particolare albero binario di ricerca. Gli elementi di un insieme A sono contenuti nei nodi di un albero ordinato D tale che:
ogni nodo interno (non foglia) ha k figli, k=2,3, e contiene k-1 elementi di A, ordinati in senso crescente.
le foglie non contengono alcun elemento di A
tutte le foglie sono allo stesso livello
se un nodo u ha k figli, allora l’elemento i-esimo di u è maggiore di tutti gli elementi contenuti nel sottoalbero la cui radice è l’i-esimo figlio di u, ed è minore di tutti gli elementi contenuti nel sottoalbero la cui radice è l’(i+1)-esimo figlio di u, per 1 <= i <= k-1.

Infatti 4 è maggiore di 2,1 e 3 e minore di 8,5,7 e 9; mentre 10 è maggiore di 8,5,7 e 9 e minore di 12,11 e 13. Sia L il livello massimo delle foglie. Nel caso peggiore ogni nodo contiene 1 solo elemento, quindi L è al più log2(n+1). Viceversa, nel caso migliore, ogni nodo contiene 2 elementi; quindi L è almeno log3(n+1). Per realizzare l’operatore “appartiene” si confronta l’elemento x da ricercare con quelli contenuti nella radice e, se l’ elemento non è presente, ma è maggiore di un i-esimo elemento e minore dell’ (i+1)-esimo, si riapplica il procedimento all’ (i+1)-esimo sottoalbero.

Per realizzare l’operatore min si compie una ricerca lungo il cammino ottenuto visitando sempre il primofiglio di ogni nodo, se questo esiste.
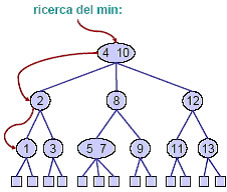
Analogamente, si può implementare l’operatore max. Per l’ operatore “inserisci” occorre effettuare una ricerca per individuare il nodo u in cui dovrebbe essere elemento (sempre a livello L-1). Se u contiene 1 solo elemento, si effettua l’inserzione nel nodo aggiungendo inoltre un nodo foglia. Se u invece contiene 2 elementi, si sdoppia u in 2 nodi fratelli contenenti un elemento ciascuno. Per rispettare l’ ordine tra nodi, il primo fratello prende il valore minimo, il secondo massimo e il valore intermedio diventa padre.

Analogamente si può implementare anche l’ operatore “cancella” anche se in modo piuttosto complicato.. Tutti questi operatori hanno una complessità O(log n). La difficoltà implementativa dell’operatore di cancellazione negli alberi 2-3 ha portato allo studio dei B-alberi binari, studio che si deve a Bayer, 1971.
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.