Analisi di reti sequenziali

Analizziamo il seguente circuito nel quale sono presenti due ingressi x₁ e x₂, due uscite z₁ e z₂, due latch di tipo S-R le cui uscite sono definite y₁ e y₂.

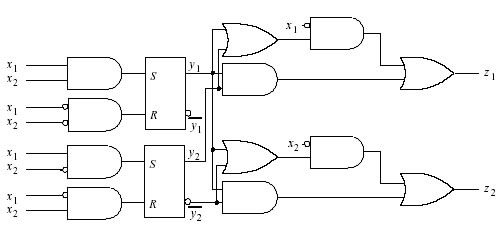
Come si può vedere, le uscite della rete sono una funzione combinatoria degli ingressi (x₁, x₂) e delle uscite dei latch (y₁, y₂), e possono pertanto essere descritte con i metodi delle reti combinatorie. In modo analogo, gli ingressi dei latch (S,R) sono funzioni combinatorie degli ingressi della rete. Il legame fra gli ingressi della rete e le uscite dei latch introduce il concetto di "memoria" tipico della rete sequenziale. Supponiamo ad esempio che in un certo istante la configurazione associata agli ingressi x₁ e x₂ sia 00 che le uscite dei latch siano di conseguenza y₁ e y₂ 00. L'ingresso x₁ passi a 1 (1000 x₁, x₂, y₁, y₂). In questo caso, anche l'ingresso S₂ al secondo latch passa a 1, e ciò comporta che l'uscita y₂ di tale latch debba a sua volta passare a 1. In altre parole, lo stato 1000 è uno stato instabile per la rete sequenziale destinato a trasformarsi nello stato stabile 1001. La cosa può essere ripetuta per tutte le configurazioni di x₁, x₂, y₁ e y₂, ottenendola seguente tabella:

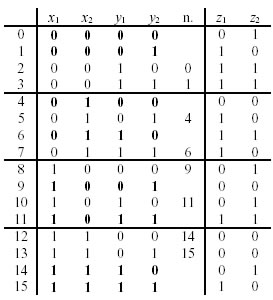
Gli stati stabili sono rappresentati in neretto, mentre i numeri accanto agli stati instabili indicano in quali stati stabili sono destinati a trasformarsi. Un modo più comodo per indicare tali transizioni fra stati instabili e stati stabili è quello di specificare, per ogni stato, il prossimo valore delle uscite dei latch (y₁ e y₂) solitamente indicato con lettere maiuscole (Y₁ e Y₂). Le uscite attuali y₁ e y₂ prendono il nome di variabili interne della rete, mentre Y₁ e Y₂ prendono il nome di variabili dello stato prossimo. Considerando che al variare degli ingressi, le entrate ai bistabili saranno:

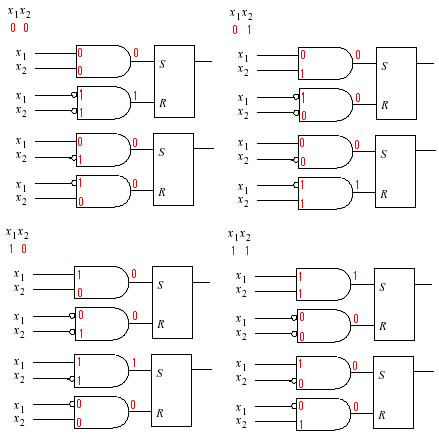
otteniamo la tabella:

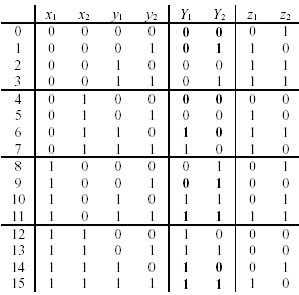
Analizziamo come esempio la riga 3: le variabili interne (y₁ e y₂) sono 11 (memoria del passato).
Applico in ingresso 00.
Resetto quindi il primo bistabile (riceve un impulso sul reset) mentre il secondo bistabile rimane inalterato: Y₁Y₂ sarà quindi 01. Un modo più usuale di indicare le stesse informazioni è quello di adottare la tabella delle transizioni insieme alla tabella delle uscite. Si tratta di tabelle nelle quali gli indici di colonna sono le configurazioni delle variabili esterne, gli indici di riga sono le configurazioni delle variabili interne attuali (cioè gli stati presenti) e i valori riportati in ciascuna casella sono rispettivamente i valori delle variabili di stato prossimo e i valori delle uscite:

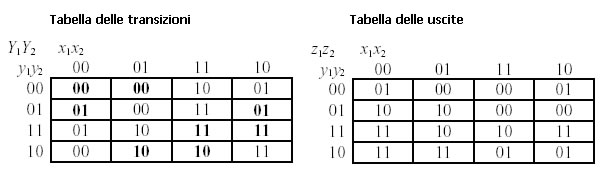
Da uno stato stabile della tabella delle transizioni, una qualsiasi variazione degli ingressi provoca uno spostamento di colonna. Se la casella in cui ci si sposta è caratterizzata da uno stato prossimo diverso dallo stato presente associato alla riga della tabella in cui ci si trova, si verifica anche uno spostamento di riga per raggiungere il nuovo stato stabile. Il funzionamento della rete sequenziale è dunque associabile ai movimenti di un "punto di lavoro" che si sposta all'interno della tabella delle transizioni. Una forma più sintetica della tabella delle transizioni è la tabella degli stati, nella quale ogni configurazione di stato presente (s) e prossimo (S) è rappresentata da una lettera:

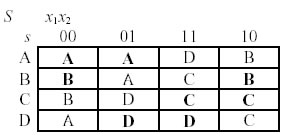
Dalla tabella delle transizioni, conoscendo le variabili interne (y₁, y₂) e le variabili dello stato prossimo (Y₁,Y₂), posso ricavare le funzioni di eccitazione, cioè le equazioni logiche che esprimono gli ingressi dei latch in funzione degli ingressi alla rete. Per l'esempio considerato, tali funzioni sono:

Le funzioni di eccitazione sono poi utilizzate per ricavare la tabella delle eccitazioni, analoga alla tabella delle transizioni salvo il fatto che ogni casella contiene gli ingressi ai latch invece delle uscite prossime:

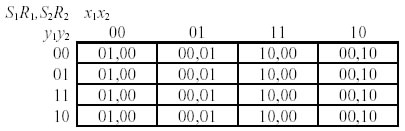
A questo punto conosciamo tutti gli elementi che contraddistinguono la nostra rete sequenziale. Si noti che in fase di progettazione di queste reti dobbiamo percorrere all'indietro i passi seguiti fino ad ora.

Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.