
 |
La tecnica di programmazione dinamica per progettare algoritmi viene introdotta da Bellman nel 1957. Essa può essere vista come un’estensione della tecnica di Divide et Impera. L’idea principale consiste nello sfruttare tutte le soluzioni dei sottoproblemi più piccoli per la costruzione dei problemi di dimensione maggiore. La Programmazione Dinamica risulta più conveniente quando i sottoproblemi non sono tra loro indipendenti. Essa risolve un sottoproblema in comune una sola volta e riutilizza la soluzione ottenuta ogni volta che è necessario. La tecnica di Divide et Impera conveniente quando i sottoproblemi sono indipendenti, evitando di ricalcolare più volte la soluzione del sottoproblema in comune. Per esempio supponiamo di dover calcolare il coefficiente binomiale, ovvero il numero di modi di scegliere k oggetti da un insieme di n oggetti, con 0 <= k <= n. Esso è definibile ricorsivamente come:
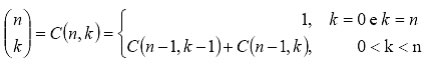
Un algoritmo ricorsivo “divide et impera” si ottiene immediatamente dalla precedente definizione ricorsiva:

La complessità dell’algoritmo ricorsivo dipende dal numero di chiamate fatte, che sono proprio C(n,k). Questo è dovuto all’ elevato numero di sottoproblemi identici che vengono risolti più volte. Per esempio C(n-2, k-1) è richiamata due volte, sia per calcolare C(n-1, k), sia per calcolare C(n-1, k-1). L’algoritmo di programmazione dinamica si basa invece sul noto schema del “Triangolo di Tartaglia”. L’ idea è quella di memorizzare in una matrice le soluzioni per dimensioni inferiori del problema, in modo di riutilizzarle per quelle di dimensione superiore.

Supponendo per esempio che il numero di componenti n sia 4 avremo una matrice di questo tipo una volta chiamata la funzione “Tartaglia”:
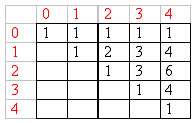
La complessità dell’algoritmo basato sullo schema di Tartaglia è O(n2), infatti il numero di assegnamenti fatti sulla matrice C è quadratico in n. Alla programmazione dinamica per essere applicabile occorre che:
Sia possibile ricombinare soluzione di problemi piccoli per ottenere quelle di problemi più grandi;
La soluzione di un sottoproblema sia invariante;
I sottoproblemi siano dipendenti.
Invece affinché la tecnica di programmazione dinamica abbia complessità al più polinomiale occorre:
un numero polinomiale di sottoproblemi da risolvere
l’ uso tabella per memorizzare soluzioni di sottoproblemi a prescindere dal loro futuro utilizzo
che il tempo per combinare le soluzioni e trovare la soluzione del problema più grande sia polinomiale
Di alcuni esempi di algoritmi che utilizzao la tecnica della programmazione dinamica:
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.