
 |
|
In matematica, grandezza definita da intensità, direzione e verso. La posizione, la velocità, l' accelerazione, le forze sono tutti esempi di grandezze vettoriali molto comuni in fisica. La differenza tra un vettore e uno scalare, cioè una grandezza definita solo da un valore che ne esprime l' intensità, si può cogliere dall'esempio che segue. Per comunicare la posizione di un oggetto servendosi di uno scalare, bisognerebbe dire solo che esso si trova a una data distanza, ad esempio 5 km; è chiaro che una tale informazione è incompleta e non sufficiente a individuare l'oggetto in questione in modo univoco: esso infatti può trovarsi in uno qualunque degli infiniti punti della circonferenza centrata nella posizione di chi parla, e di raggio 5 km. Ricorrendo a una stima vettoriale, invece si può specificare che l'oggetto si trova ad esempio a 5 km nord. Ciò equivale a descrivere la posizione sotto forma di un vettore di cui viene assegnata l'intensità (6 km), la direzione (nord-sud) e il verso (nord). Un vettore a viene rappresentato mediante una freccia avente lunghezza proporzionale all' intensità o modulo di a e direzione e verso uguali a quelli di a:

Poiché i vettori sono quantità dotate di direzione oltrechè di modulo, devono essere sommati in maniera speciale. Di seguito due modi distinti per sommare due vettori:

Nel metodo coda punta il procedimento è il seguente: in un grafico tracciate in scala uno dei vettori, detto V1; quindi tracciate il secondo vettore V2 ponendo la sua coda sulla punta del primo vettore; la freccia tracciata dalla coda del primo vettore alla punta del secondo rappresenta la somma dei vettori. Questo metodo può essere esteso a tre o più vettori. Nel metodo del parallelogramma i due vettori da sommare sono tracciati da una stessa origine, quindi viene costruito un parallelogramma usando questi due vettori come lati adiacenti. Il vettore risultante è la diagonale tracciata a partire dalla comune origine. La sottrazione di due vettori avviene in modo analogo:

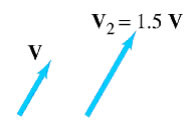
Un vettore V può anche essere moltiplicato per uno scalare c. Tale prodotto viene definito come un nuovo vettore che ha la stessa direzione di V, lo stesso verso di V, e modulo uguale a c moltiplicato per il modulo di V (cV). Se c è uno scalare negativo il modulo rimane cV, la direzione rimane la stessa, ma cambia il verso. Per esempio se moltiplico al vettore V uno scalare c = 1.5 graficamente ottengo:
Ogni vettore V può essere espresso come la somma di due altri vettori, i cui moduli sono chiamati le componenti del vettore originale. Le componenti sono solitamente scelti il modo di essere allineate lungo due direzioni perpendicolari tra loro. Il processo di ricerca delle componenti è conosciuto col nome di scomposizione del vettore nelle sue componenti. Di seguito l' esempio della scomposizione del vettore V.
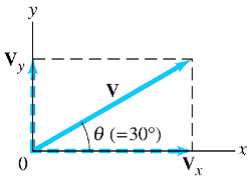
Si noti che per le proprietà della trigonometria:
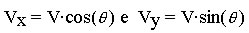
Vediamo un esempio:

Si noti che il modulo del vettore V può essere calcolato con il teorema di Pitagora. Nel caso in cui lo spazio sia tridimensionale è necessario scomporre un vettore nelle componenti lungo le tre direzioni perpendicolari tra loro.
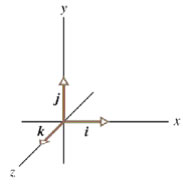
e considerando i versori i, j, k come vettori con modulo unitario (cioè 1) avremo che il vettore V potrà essere definito come:

dove la direzione del vettore prodotto è perpendicolare a quella dei due vettori, e il verso è calcolato con la regola della mano destra.
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.