
 |
Di fronte al problema di capire il mondo , gli scienziati cercano di trovare relazioni tra le varie grandezze o quantità che osservano e misurano. L' accuratezza delle misure rappresenta un aspetto importante della fisica, ma nessuna misura è precisa in assoluto. Esiste infatti un' incertezza associata ad ogni misura. Gli errori di misurazione sono dovuti a molteplici fattori. Tra i più importanti c' è la limitata accuratezza di ogni sistema di misura, e i limiti umani nel rilevare particolari misurazioni (misure molto piccole per esempio). I tipi di errori di misurazione possono essere divisi in due categorie:
Errori sistematici: gli errori eliminabili, dovuti per esempio alla taratura insufficiente di uno strumento di misura;
Errori casuali: gli errori non eliminabili.
Si può ridurre l' effetto degli errori casuali calcolando la media di N misure:
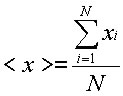
e la loro varianza:
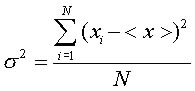
La varianza è un indicatore di dispersione, ovvero tanto più le N misure rilevate si allontanano dalla media, tanto maggiore sarà la varianza, e viceversa. La varianza è nulla solo nei casi in cui tutti i valori sono uguali tra di loro (e pertanto uguali alla loro media) e cresce con il crescere delle differenze reciproche dei valori. Spesso viene però utilizzata la deviazione standard che è anch'esso un indice di dispersione derivato direttamente dalla varianza. Il termine deviazione standard è stato introdotto in statistica da Karl Pearson nel 1894. Se non indicato diversamente, è semplicemente la radice quadrata della varianza:
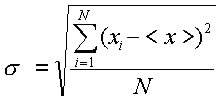
Il vantaggio della deviazione standard è che ha la stessa unità di misura dei valori osservati (mentre la varianza ha come unità di misura il quadrato dell' unità di misura dei valori di riferimento). Una volta stabilita la consistenza dell' errore di misurazione, diventa importante stabilire la precisione o l' incertezza della misura stessa. Viene quindi calcolata un' incertezza percentuale:
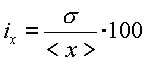
che viene usata con la media per comunicare il valore più probabile della grandezza misurata ottenuto mediante N misurazioni:
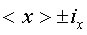
Per esempio il valore di resistenza elettrica di un resistore può essere scritto come: R = 100 ± 10% ohm. Ciò significa che se misuro la resistenza di R posso ottenere qualunque valore tra 90 e 110 ohm, con maggiore probabilità di ottenere 100. Riportando i valori delle N misurazioni in un istogramma otteniamo una qualcosa del genere:
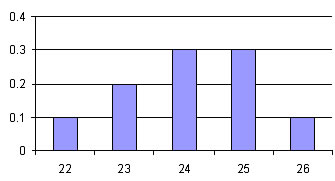
Per N molto grande l' istogramma tende ad una funzione di distribuzione di probabilità di Gauss (curva di Gauss), che al variare della deviazione standard avrà un aspetto di questo tipo:

Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.