|
|
Sappiamo che nel campo reale non esiste alcun numero che soddisfi l'equazione x2 + 1 = 0 . L'equazione ci suggerisce però due possibilità: dire che l'equazione non ammette soluzioni o ampliare il campo reale introducendo un numero "immaginario puro" che per definizione è
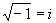
Il numero immaginario gode delle proprietà:
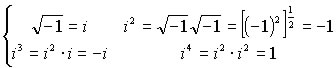
Oltre i4 le potenze di i diventano cicliche. In questo modo possiamo risolvere equazioni le quali soluzioni non saranno contenute nell'insieme dei numeri reali, ma in quello dei numeri complessi.
In tal modo abbiamo costruito due numeri che si chiamano numeri complessi e sono la somma di un numero reale e un numero immaginario. Rappresentazione algebrica: z = a + ib. Dove a rappresenta la parte reale e b quella immaginaria.
Di seguito un esempio del calcolo di una qualsiasi potenza di i
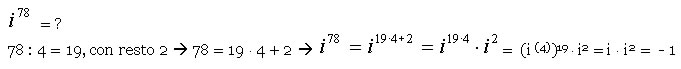
Per trovare gli algoritmi che ci permetteranno di calcolare la somma tra numeri complessi poniamo:
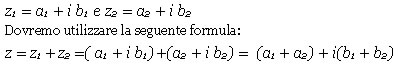
La parte reale ed il coefficiente della parte immaginaria andranno sommati distintamente, quindi la somma di due numeri complessi darà sempre un numero complesso. Per la somma valgono le proprietà associativa e commutativa, quindi:
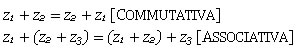
Per individuare un metodo per calcolare il prodotto tra numeri complessi poniamo ancora:
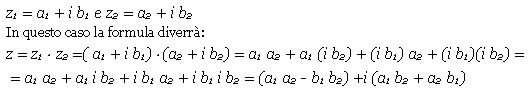
Anche il prodotto gode delle proprietà associativa e commutativa. Quindi:
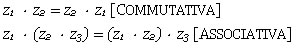
Qualsiasi numeri complesso sarà sempre riconducibile alla forma algebrica z = a + ib .
Si chiama complesso coniugato di z e si indica con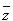 
il numero complesso: 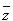= a - ib
Per saperne di più consulta i seguenti approfondimenti:
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.