
 |
Gli automi a stati con memoria limitata, e comunque finita poiché hanno un numero finito di stati: sono chiamati automi a stati finiti. Più precisamente definiamo automa a stati finiti un sistema dinamico, discreto ed invariante, in cui gli insiemi d’ingresso, di uscita e di stato sono finiti. Il sistema può trovarsi in un qualsiasi stato interno fra quelli, in numero finito, che definiscono l’automa. Una classe di automi particolarmente importante è quella degli automi in grado di riconoscere se una stringa fa parte o meno di un determinato linguaggio: automi riconoscitori. Gli automo riconoscitori, in pratica, sono sistemi che, dopo l’ingresso dell’ultimo simbolo della sequenza, rispondono con un "si" se questa è stata riconosciuta e con un "no" in caso contrario. Un automa a stati finiti di questo tipo consiste di un insieme finito di stati e di un insieme finito di transizioni da uno stato all’altro. Per ogni coppia distinta formata da uno stato dell’automa (stato di partenza) e da un simbolo dell’alfabeto, esiste una transizione ad uno stato di arrivo. Il simbolo della coppia si dice associato alla transizione, o anche che la transizione "accetta il simbolo". Lo stato di arrivo può anche coincidere con lo stato di partenza. Ogni automa a stati finiti è associato univocamente ad un grafo orientato (in inglese direct graph) chiamato diagramma di transizione (in inglese transition diagram). I nodi del grafo coincidono con gli stati dell’automa. Se esiste una transizione dallo stato q allo stato p con a come simbolo associato, allora esiste un arco orientato dal nodo q al nodo p ed etichettato con il simbolo a. Per questa ragione gli automi a stati finiti vengono anche detti reti di transizione a stati finiti (FSTN, finite state transition network, in inglese). Si dice che il grafo accetta la stringa x, costruita con i simboli dell’alfabeto predeterminato, se esiste una sequenza di transizioni tali che, componendo la sequenza dei rispettivi simboli associati, si ottenga x. Inoltre la prima transizione di questa sequenza deve partire dallo stato iniziale e l’ultima arrivare ad uno stato finale. Anche molti modelli astratti usati per rappresentare sistemi molto complessi come i sistemi economici, le reti di neuroni, i problemi d trasporto, e così via, possono essere agevolmente rappresentati attraverso automi a stati finiti. Per descrivere un automa occorre un modello matematico formato dalla quintupla:
A = {S, I, U, f, g}
dove:
S è l’insieme degli stati interni in cui può trovarsi;
I è l’insieme degli ingressi che è in grado di leggere;
U è l’insieme delle uscite che può produrre;
f è la funzione che fa passare da uno stato al successivo
g è la funzione che determina il valore delle uscite
Diamo ora un esempio di un automa che accetta solo stringhe con un numero pari di 1 o di 0. Un modo per definire l’automa è tracciare il diagramma di transizione. Gli stati cerchiati due volte sono stati finali.

Definiamo di seguito l’automa con una tabella detta tabella degli stati costruita in questo modo: ogni riga è associata a uno stato q di partenza, ogni colonna ad un simbolo a, che in questo caso varrà uno o zero.

Il tipo di automa così definito viene detto deterministico, perché per ogni stato è sempre possibile determinare univocamente quale transizione l’automa effettui all’ingresso di un dato simbolo. Far cadere il vincolo che per ogni stato esista sempre una ed una sola transizione associata ad un simbolo è equivalente ad affermare che possono esistere zero, una, o più transizioni che partono dal medesimo stato con il medesimo simbolo di ingresso. In questo caso non è sempre possibile determinare univocamente quale transizione l’automa effettui all’ingresso di un dato simbolo. L’automa si dice non deterministico. Per esemplificare definiamo un automa non deterministico che accetta qualsiasi stringa che contenga una coppia di 0 o di 1. Il diagramma di transizione è analogo con la differenza che gli archi hanno liste di simboli come etichette.
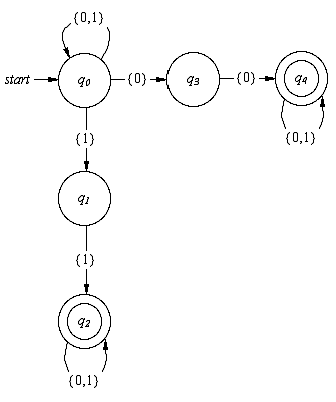
La tabella degli stati sarà:

Il linguaggio accettato da un automa a stati finiti è l’insieme di tutte le stringhe accettate dall’automa.
Per saperne di più consulta i seguenti approfondimenti:
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.