Metodo di Gauss-Jordan

Metodo utilizzato per risolvere sistemi lineari per mezzo delle matrici. Si consideri un sistema lineare di m equazioni in n incognite, i cui coefficienti siano in un campo qualsiasi (Q, R, Zp )

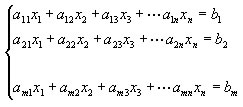
Il sistema può essere pensato come un prodotto di matrici:

Chiamiamo matrice dei coefficienti del sistema la matrice A (m righe e n colonne), vettore delle incognite il vettore x, vettore dei termini noti il vettore b.
Chiamiamo infine matrice completa del sistema la matrice a m righe e n+1 colonne:

Senza cambiare le eventuali soluzioni del sistema, si può agire sulla matrice con le seguenti operazioni:
Scambiare due righe tra loro.
Moltiplicare una riga per una costante non nulla.
Sommare ad una riga il multiplo di un'altra riga.
Eliminare una riga se composta totalmente da 0.
(tutte queste operazioni, se pensate applicate al sistema, le cui equazioni corrispondono alle righe della matrice, portano ad un sistema equivalente, cioè con le stesse soluzioni).
Il metodo di Gauss-Jordan per la risoluzione del sistema consiste nei seguenti passi:
se a₁₁= 0 si scambia la prima riga con le successive fino ad ottenere a₁₁0, quindi si somma ad ogni riga (da 2 a m) un opportuno multiplo della prima in modo da ottenere a_ki=0 per ogni k1.
se a₂₂=0 si scambia la seconda riga con le successive fino ad ottenere a₂₂0, quindi si somma ad ogni riga (esclusa la seconda) un opportuno multiplo della seconda in modo da ottenere a_k2=0 per ogni k2.
Si continua allo stesso modo su tutte le righe. Se nella sequenza delle operazioni si ottiene una riga di 0, la si elimina. Al termine del procedimento la matrice può essere solo di uno dei tre seguenti tipi:

potrebbero esserci anche più righe come l'ultima, ma il discorso non cambia. In questo caso, poiché b_n+10 (altrimenti la riga sarebbe stata eliminata), il sistema non ha alcuna soluzione. Vi è poi un terzo caso in cui il sistema ha ^n-k soluzioni, cioè infinite soluzioni dipendenti da n-k parametri.
Questo metodo consente anche di calcolare la matrice inversa, per saperne di più consulta gli approfondimenti:

Calcolo della matrice inversa col metodo di Gauss-Jordan.

Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.