
 |
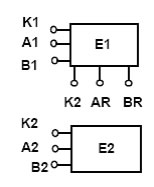
Associazione binaria 1 a N indica che la cardinalità dell' associazione è da una parte del tipo (1,1) o (0,1) e dall' altra (1,n). Supponiamo di avere uno schema E-R del seguente tipo, e di eseguire una traduzione standard verso il modello logico.

Otteniamo col metodo standard tre relazioni. Utilizzando metodi
non tradizionali si può fare di meglio. Se E1 partecipa con cardinalità (1,1)
può essere fusa con l'associazione, ottenendo una soluzione a due relazioni:
E1(K1, A1, B1,K2, AR, BR)
E2(K2, A2, B2)
Se E1 partecipa con cardinalità (0,1) la soluzione a due relazioni ha valori
nulli in K2, AR, BR per le istanze di E1 che non partecipano all'associazione.
Si avrà quindi due entità:
Attenzione, poiché la partecipazione di E1 è 0,1 o 1,1, si
nota facilmente che ad un dato valore di K1 corrisponde uno e un sol valore
di K2 (non è vero il contrario). Quindi si può dire che K1 implica K2 o, anche,
che esiste una dipendenza funzionale da K1 a K2. In questo
caso nella soluzione a 3 relazioni la chiave della relazione che traduce l'associazione
è riducibile a K1 ottenendo il seguente risultato.
E1(K1,A1,B1)
E2(K2,A2,B2)
R(K1,K2,AR,BR)
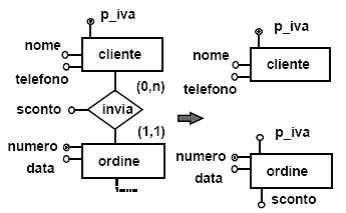
Un esempio di un associazione binaria 1 a N senza attributi sull' associazione è:

Oppure un ulteriore esempio con attributi sull'associazione:
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.