
 |
Ramo della matematica basato sul calcolo logico a due valori di verità (vero, falso). Con alcune leggi particolari consente di operare su proposizioni allo stesso modo che su entità matematiche. L'algebra Booleana dal matematico inglese Boole, trova numerose applicazioni nelle scienze fisiche, in particolare nel campo dei computer e dell'elettronica. Oggi infatti questa algebra chiamata anche "algebra di commutazione", fornisce strumenti per la modellizzazione e la trattazione di dispositivi basati su logica binaria. Questo in quanto le grandezze che possono assumere solo due valori, possono facilmente essere associate ai dispositivi elettrici di un circuito digitale binario (dal momento che tali dispositivi sono realizzati in modo tale da assumere solo due stati elettrici estremi). Mediante l'algebra di commutazione, è possibile effettuare una progettazione logica dei dispositivi, trascurando il modo in cui verranno fisicamente realizzati. L'algebra booleana è basata sui seguenti POSTULATI: definiamo come X una qualsiasi variabile binaria. Il primo postulato afferma semplicemente che trattiamo logica binaria.

Definiamo ora che esiste un segnale avente valore opposto di quello assunto dalla variabile X.

Sulle variabili logiche così introdotte, si possono definire le operazioni di inversione (o negazione, o NOT, indicata dal tratto sopra il nome della variabile), di prodotto logico di due variabili (o operazione AND, indicata dal simbolo •, a volte omesso come nell'algebra comune), di somma logica di due variabili (o operazione OR, indicata dal simbolo +). I seguenti tre postulati definiscono le operazioni di prodotto e somma logici:

Si noti che i postulati sono stati definiti sempre a coppie, il cui secondo membro è stato indicato da un apostrofo ('). Si noti anche che ciascun secondo membro è ottenibile dal primo mediante scambio dei valori 0 e 1 e scambio degli operatori · e +. Questo è un esempio del principio di dualità, vero per tutti i teoremi dell'algebra di commutazione poiché risulta vero per i suoi postulati. Da questi postulati si ricavano i seguenti teoremi, dimostrabili semplicemente sostituendo alle variabili tutti i possibili valori (0 e 1):


Dei teoremi a n variabili citiamo quello di De Morgan:
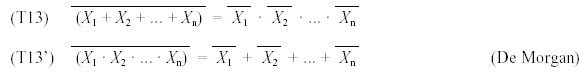
Le operazioni logiche fondamentali viste fino ad ora: NOT (negazione), OR (+) e AND (•), sono realizzabili fisicamente da dispositivi elementari costituiti da transistor. Questi "circuiti minimi" prendono il nome di porte logiche. La porta NOT nega o inverte il segnale ricevuto, la porta OR ne fa la somma logica, e la AND il prodotto logico. Funzioni booleane, ovvero funzioni di variabili booleane (assumono soltanto i valori vero e falso 1,0), possono essere realizzate con gruppi di porte logiche interconnesse opportunamente tra loro creando cosi un vero e proprio circuito digitale chiamato rete logica. Il vantaggio dell'algebra di Boole sta nel fatto che applicando i suoi teoremi permettere la semplificazione di questi circuiti digitali senza doverli realizzare fisicamente.
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.