|
|
Prima di introdurre la nozione di derivata, è necessario premettere qualche richiamo sull'equazione di una retta nel piano cartesiano. In un piano cartesiano per individuare una retta è necessario assegnare due punti distinti A e B.
Vogliamo caratterizzare tutti i punti del piano che appartengono alla retta passante per A e B. Dalla similitudine dei triangoli rettangoli AXQ e ABR si ricava la relazione di proporzionalità tra i cateti:
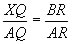
Passando alle coordinate dei punti si ricava:
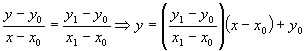
La relazione precedente costituisce l'equazione della retta passante per due
punti assegnati A e B. La quantità
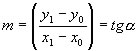
si chiama coefficiente angolare della retta,
ed uguale alla tangente dell'angolo che la retta forma con l'asse delle ascisse.
L'equazione della retta diventerà:
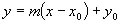
Si tratta ora di vedere come si può costruire una retta tangente alla funzione y = f(x) in un punto x0 del dominio. Supponiamo che il grafico della funzione sia il seguente:
Si tratta ora di determinare tra tutte le infinite rette passanti
per il punto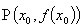 
, quella che è tangente alla funzione in P. Sia
P' un altro punto di f(x) di coordinate 
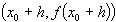. P' è chiamato il punto variato rispetto
a P. Avendo a disposizione due punti P e P', siamo in grado di costruire la
retta passante per essi:
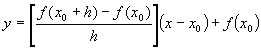
a questo punto per ottenere la tangente alla curva facciamo avvicinare il punto P' al punto P, il che equivale a far diventare h prossimo al valore zero. Nell'equazione della retta l'unica quantità che dipende da h, è il coefficiente angolare della retta. Pertanto passando al limite si ha:
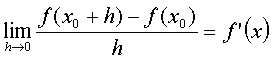
La quantità appena definita si chiama derivata prima della funzione y = f(x) valutata in un punto x0 del dominio. In tale modo risulta evidente anche il significato geometrico della derivata prima, ovvero il coefficiente angolare della retta tangente in un punto della curva. L'equazione della retta può quindi essere scritta:
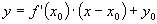
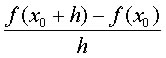
si chiama rapporto incrementale di f(x) nel punto iniziale x0 e incremento h.
Per saperne di più consulta i seguenti approfondimenti:
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.