Minimizzazione di reti combinatorie

Per minimizzare una rete combinatoria è necessario trovarne gli implicanti, ovvero prodotti logici che derivano da un gruppo di mintermini che hanno la proprietà di avere una parte comune e un'altra parte che assume tutte le possibili combinazioni. In modo duale un implicato è una somma logica che deriva da un gruppo di maxtermini che hanno la proprietà di avere una parte comune e un'altra parte che assume tutte le possibili combinazioni. Vediamo un esempio:

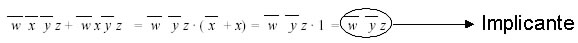
Gli implicanti posso derivare da gruppi di 2, 4, 8 ,16 mintermini:

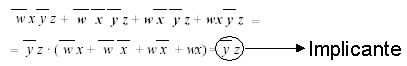
Naturalmente più il gruppo di mintermini è grande maggiore sarà la minimizzazione. I prodotti logici che derivano dai gruppi di mintermini maggiori che hanno la proprietà di avere una parte comune e un'altra parte che assume tutte le possibili combinazioni si dicono implicanti primi. Per gruppi di mintermini maggiori si intende gruppi che non sono contenuti in nessun altro gruppo. Vediamo un esempio:

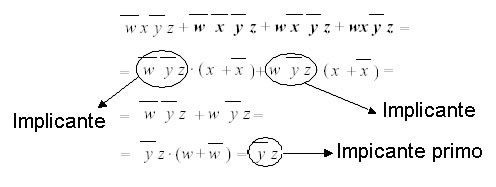
Un implicante primo è quindi un implicante non contenuto in nessun implicante di dimensioni maggiori. Dobbiamo quindi ricercare tutti gli implicanti primi della funzione booleana che vogliamo minimizzare. A questo scopo utilizziamo la rappresentazione geometrica dei numeri binari. Le configurazioni binarie sono rappresentabili come n-cubi in uno spazio a n dimensioni (ipercubo). La costruzione di un n-cubo è una operazione ricorsiva, nella quale si proietta una copia di un n-cubo, e si aggiunge 0 a tutti gli identificatori degli elementi dell'n-cubo di partenza, e si premette un 1 a tutti gli identificatori degli elementi dell'n-cubo proiettato. Lo 0-cubo è un punto privo di identificatore.

Si noti che i punti di un n-cubo sono connessi con punti a distanza di Hamming unitaria e ogni vertice di un n-cubo è collegato ad altri n vertici. Per esempio ogni vertice di un 2-cubo è collegato ad altri 2 vertici, ogni vertice di un 3-cubo è collegato ad altri 3 vertici e cosi di seguito. Un p-sottocubo di un n-cubo è l'insieme di 2^p punti aventi (n-p) bit corrispondenti, mentre gli altri assumono tutte le possibili configurazioni. Per esempio un 2-cubo (che è un sottocubo di un 3-cubo) è l'insieme di 2² = 4 punti aventi n-p = 3-2 = 1 bit corrispondente, mentre gli altri assumono tutte le possibili configurazioni:

Proviamo ora ad analizzare la seguente tabella delle verità:

La somma canonica SP della funzione specificata è la seguente:

Sostituiamo nel 4-cubo le configurazioni di bit in ingresso (w,x,y,z) con il valore della funzione f all'uscita.

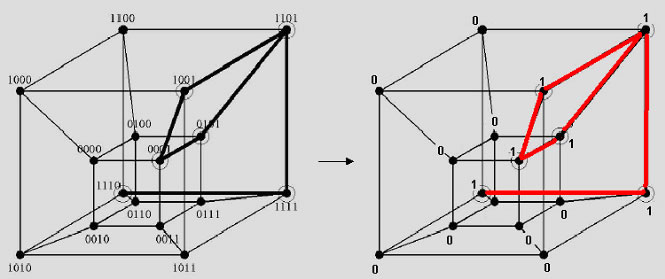
Unendo i vertici in cui l'uscita f assume valore 1, otteniamo 3 sottocubi (un 2-cubo e due 1-cubo). Grazie alla proprietà sopra citata dei sottocubi, e cioè che un p-sottocubo di un n-cubo è l'insieme di 2^p punti aventi (n-p) bit corrispondenti, mentre gli altri assumono tutte le possibili configurazioni, possiamo scrivere che:

Dai sottocubi, i cui vertici assumono tutti valore 1 derivano i gruppi di mintermini dai quali si possono ricavare gli Implicanti.
Dai sottocubi , i cui vertici assumono tutti valore 0 derivano i gruppi di maxtermini dai quali si possono ricavare gli Implicati.
Dai sottocubi di dimensioni maggiori si ricavano gli implicanti primi.

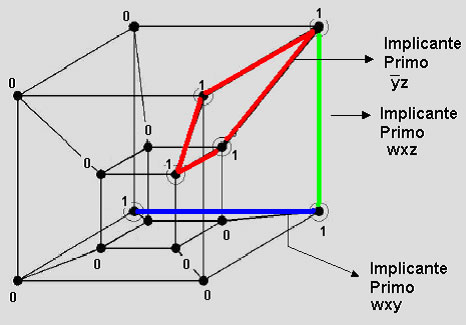
Nel caso della SP confrontando i vertici dei sottocubi individuati si prendono le sole variabili (w,x,y,z) che variano negandole se sono a 0, e prendendole diritte se sono a 1. Nel caso della PS confrontando i vertici dei sottocubi individuati si prendono le sole variabili (w,x,y,z) che variano negandole se sono a 1, e prendendole diritte se sono a 0. La nostra funzione booleana espressa come SP sarà quindi:

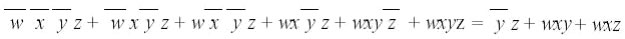
La funzione cosi ottenuta, inserendo tutti gli implicanti primi, non è però la più semplice ottenibile. La somma minima deve infatti contenere solo implicanti primi, ma non necessariamente tutti gli implicanti primi presenti. Per identificare quali prodotti devono essere presenti nella somma minima, si può ricorrere al concetto di implicanti primi essenziali: viene definito implicante primo essenziale un implicante primo che abbia la caratteristica di contenere almeno un mintermine non contenuto in nessun altro implicante primo (cioè un implicante primo che "copra" almeno un mintermine non coperto da altri). Sicuramente, ogni implicante essenziale deve essere contenuto nella somma minima. Qualora rimangano mintermini isolati non coperti da nessun implicante essenziale, si includono scegliendo i maggiori implicanti primi che li coprono. La funzione minima sarà quindi:

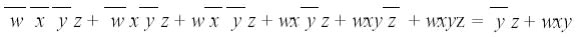
Questo metodo di minimizzazione di reti combinatorie può risultare macchinoso se ogni volta dobbiamo disegnare un n-cubo ed inoltre la rappresentazione in uno spazio a n dimensioni non è maneggevole. Per rendere più semplificata la minimizzazione si è quindi pensato di "aprire" su un piano questi n-cubi (sviluppo nel piano dei cubi), creando cosi delle mappe chiamate mappe di Karnaugh. Queste sono molto utilizzate per minimizzare reti combinatorie a quattro variabili (al massimo sette o otto), nel caso di più variabili viene utilizzato il metodo tabellare (Quine-McCluskey). Vedi:

Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.