
 |
Una mappa di Karnaugh si può ottenere sviluppando su un piano un n-cubo.

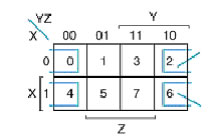
In base al numero di vertici dell' n-cubo la mappa avrà n celle. La mappa di Karnaugh ricavata "aprendo" un 2-cubo avrà 4 celle, e rispettando le adiacenze avremo:

La mappa di Karnaugh ricavata "aprendo" un 3-cubo avrà 8 celle:

Ogni vertice di un n-cubo è collegato ad altri n vertici. Per esempio m3 (ottenuto con la stringa di bit in ingresso 110) è collegato con m7(111), m2(100), e m1(010). Ma m0(000) con cosa è collegato? Andando a vedere la rappresentazione grafica del 3-cubo si nota che il vertice 000 è collegato a 001, a 100 e a 010.

Analizzando tutti i casi si ottiene che le celle 0-2, 4-6 sono adiacenti:
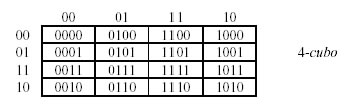
La mappa di Karnaugh ricavata "aprendo" un 4-cubo avrà 16 celle.

Andando a vedere la rappresentazione grafica del 4-cubo e analizzando tutti i casi si ottiene che le celle 0-4-12-8 sono adiacenti alle celle 2-6-14-10, le celle 0-1-3-2 sono adiacenti alle celle 8-9-11-10 e che 0-2-8-10 sono adiacenti tra loro (8 è adiacente a 10-0-9-12 ecc…).
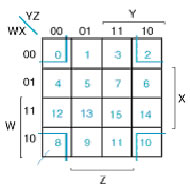
In ogni casella si trascrive il valore assunto dalla funzione quando la configurazione delle variabili corrisponde a quella delle coordinate che contrassegnano le caselle. Se si utilizza la forma canonica SP (somma di prodotti, cioè somma canonica di mintermini) si nota che due uni situati in due caselle adiacenti corrispondono a due mintermini nei quali si possono raccogliere a fattore comune le variabili che non cambiano valore nelle espressioni dei due mintermini, eliminando invece l'unica variabile che cambia valore e ottenedo cosi un implicante. Allo stesso modo, quattro uni situati in caselle disposte a quadrato o allineate corrispondono a quattro mintermini nei quali si possono raccogliere a fattore comune le variabili che non cambiano valore nelle espressioni dei due mintermini, eliminando invece le uniche due variabili che cambiano valore e ottenendo cosi un implicante. Lo stesso discorso è valido anche per otto o sedici uni situati in caselle adiacente. A questo punto posso ricercare tutti gli implicanti primi essenziali e minimizzare la rete combinatoria. Supponiamo di avere la funzione espressa come somma di mintermini: f(a,b,c,d) = E(4,5,6,12,13). Nella K-mappa la rappresentazione si ottiene mettendo 1 nella cella corrispondente al mintermine:
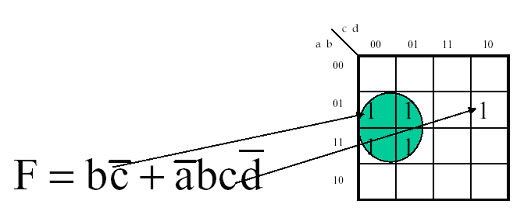
Un altro esempio:
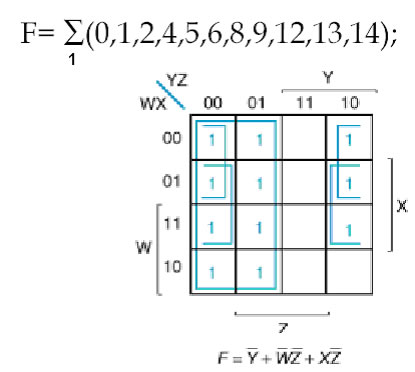
Un esempio di PS ( si comporta in modo duale):
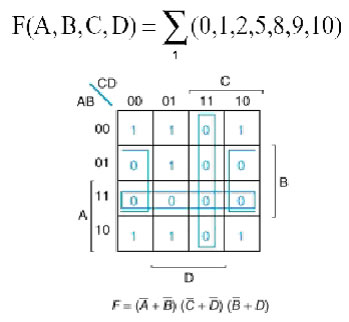
La tecnica di minimizzazione con mappe di Karnaugh si può applicare
anche a funzioni con 5 o 6 variabili, per saperne di più vedi:
Minimizzazione con mappe di Karnaugh di reti con 5 o 6 ingressi.
Tutto quanto riportato in questa pagina è a puro scopo informativo personale. Se non ti trovi in accordo con quanto riportato nella pagina, vuoi fare delle precisazioni, vuoi fare delle aggiunte o hai delle proposte e dei consigli da dare, puoi farlo mandando un email. Ogni indicazione è fondamentale per la continua crescita del sito.